Topological braiding and information processing dynamics during cell signaling
The concept of topology being an elegant yet key determinant of physical systems has been an important one brought up in modern physics research. It is across diverse complex matter fields that such claim has found unexpected yet solid evidence, and the biological constitutes of molecules, cells and organisms are extradinary examples of them. The application of topological measures in living systems offers an perspective unprecedented in its potential to tame their complexity and diversity, by connecting unversalities across model systems. Despite the promising faces, such measures are still in development especically in terms of their connection to math formalism and biological implications.
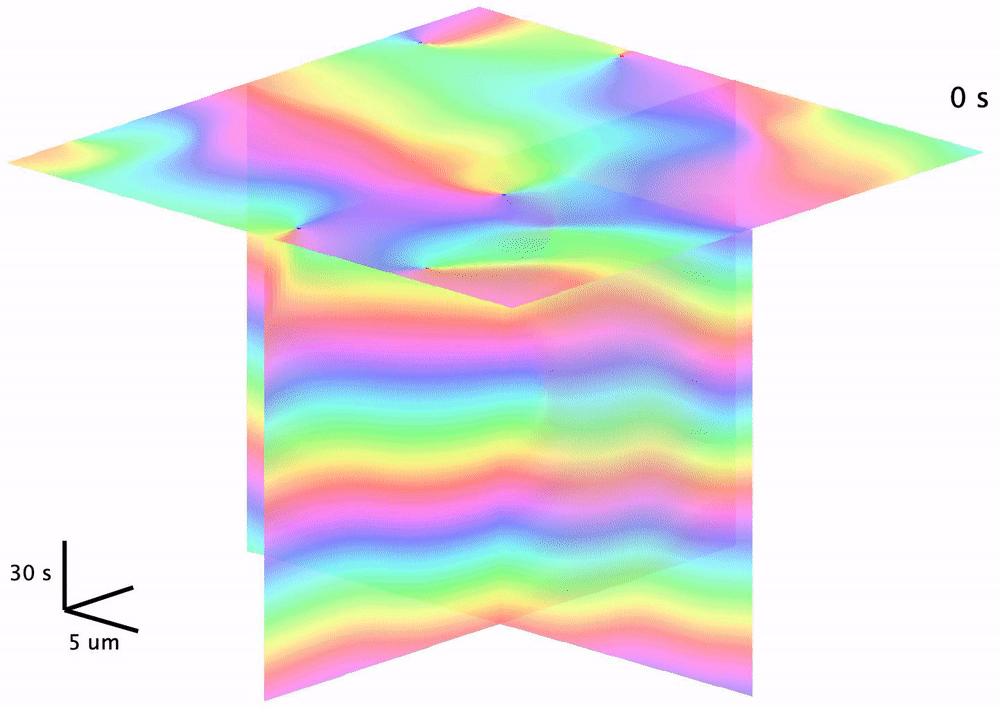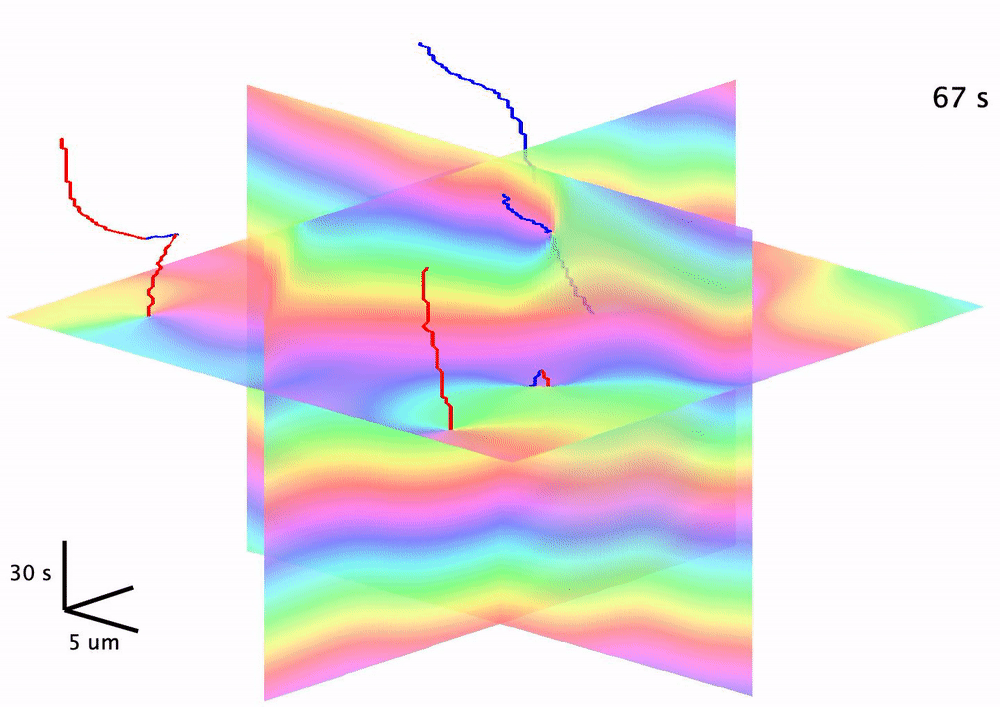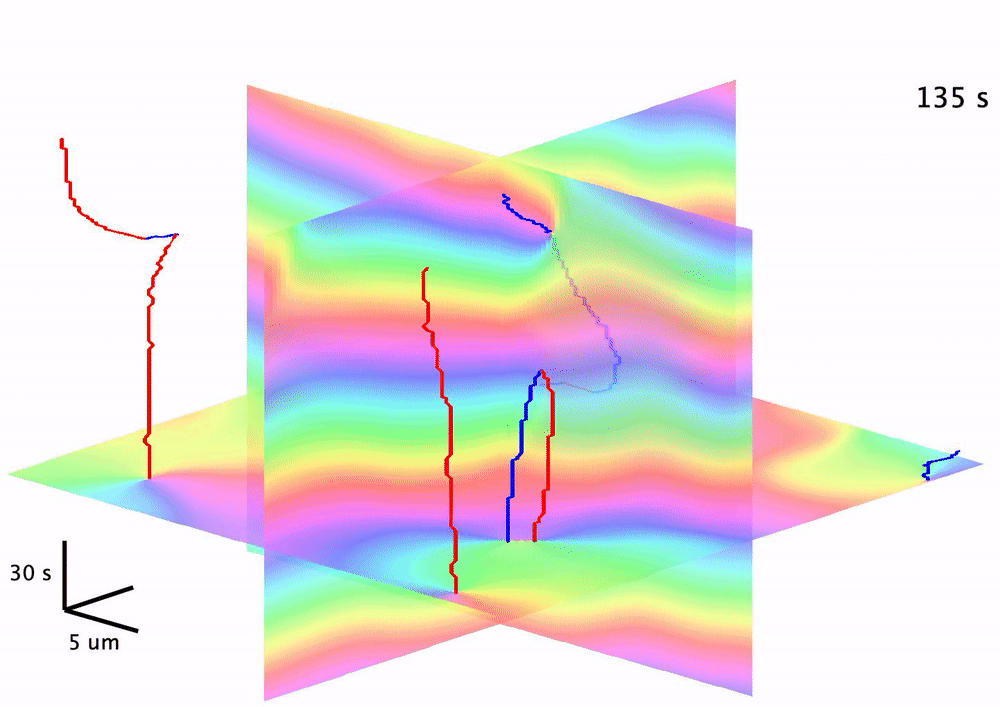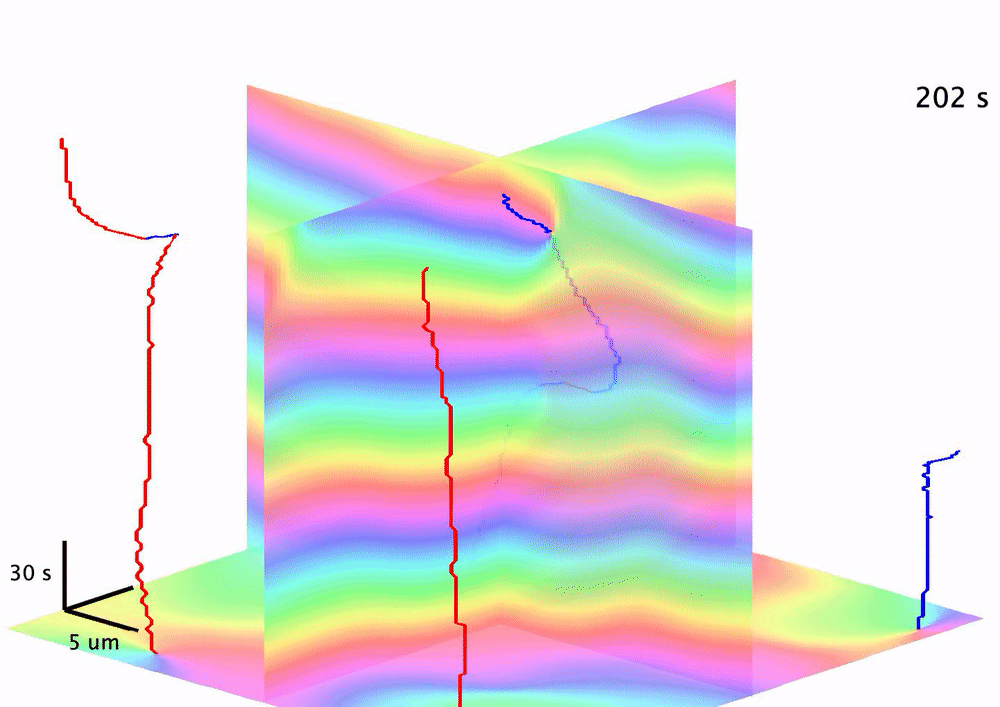
We moved further such an application via characterizing the topological braiding dynamics and quantifying its close correspondence to information processing dynamics during cell signaling. Studying the Rho-GTP signaling wave patterns formed during sea star egg cell development, we found that the Rho-GTP activity level critically determines the topological order parameters extratable from space-time phase continuum. More intriguingly, applying an established math formalism of calculating growth of topology entropy (braiding exponent), we found that such activity levels give rise to sequential rises in both the braiding exponent growth and the information loss rate. We therefore provide a first-of-its-kind case study of topological quantification with implications in understanding the propagation of live-cell signaling information.
Check here for the in-revision project: J. Liu, J. F. Totz, P. W. Miller, A. D. Hastewell, J. Dunkel, N. Fakhri..